PILASTRI SOGGETTI A SFORZO NORMALE CENTRATO

---

Premessa e brevi richiami sulla teoria del cemento armato

Fra le tante ipotesi su cui si fonda la teoria del cemento armato, una delle più importanti consiste nella aderenza tra l'acciaio ed il calcestruzzo. I due materiali possiedono un coefficiente di dilatazione termica quasi uguale: 0,000012 l'acciaio e 0,000010 il calcestruzzo.

Pertanto, in un elemento strutturale in c.a. soggetto a dilatazione termica non si determinano, di massima, stati tensionali e reciprochi scorrimenti nei due materiali. La conseguenza sostanziale di tale osservazione è che le deformazioni unitarie nell'acciaio (e_a) e nel calcestruzzo (e_b), in un elemento che si deformi sotto carico, sono uguali:

e_a = e_b (a)

e poiché in campo elastico entrambi i materiali seguono la legge di Hooke che, come è noto, pone in relazione di diretta proporzionalità gli sforzi e le deformazioni (s = E*e, essendo E il modulo di elasticità longitudinale o modulo di Young), si avrà:

e

e dalla (a) si perviene alla relazione:

da cui si ottiene

dove "m" rappresenta il coefficiente di omogeneizzazione tra l'acciaio ed il calcestruzzo che l'attuale regolamento pone uguale a 15.

Dalla relazione fondamentale soprascritta moltiplicando entrambi i membri per un qualsiasi valore A_a di acciaio, si ottiene:

La quantità dentro parentesi, al secondo membro, ci suggerisce che un'area (mA_a) di calcestruzzo è idonea ad assorbire lo stesso sforzo di un'area di acciaio A_a collocata nella medesima posizione di questa. Ciò giustifica la denominazione di coefficiente di omogeneizzazione attribuita ad "m" che consente di trattare il cemento armato come un materiale omogeneo costituito solo da calcestruzzo tanto nella zona compressa quanto nella zona tesa, dove sostituisce l'acciaio nella sua posizione con un'area equivalente pari ad "mA_a".

Si ricorda che il modulo di elasticità longitudinale dell'acciaio vale E_a = 2.100.000 kg/cmq, mentre quello del calcestruzzo, in assenza di sperimentazione diretta, vale .

Norme regolamentari

1) tensioni ammissibili:

quando il lato minore del pilastro "s" risulta inferiore a 25 cm, la tensione ammissibile si riduce a:

2) pilastri a sezione rettangolare:

Acsn	area di calcestruzzo strettamente necessaria	Acsn = N/sb
Ac	area della sezione di calcestruzzo	Ac = B*H
Aci	area ideale del calcestruzzo	Aci = Ac + m Aa
m	coefficiente di omogeneizzazione	m = 15
Aa	armatura longitudinale	Aa ³ 0,8% Acsn
		0,3% Ac £ Aa £ 6% Aa
Aa min	armatura longitudinale minima (una barra per ogni spigolo)	4 F 12 = 4,52 cmq
Ast	armatura trasversale - staffe	Fmin ³ 6 mm
		Fmin ³ 1/4 Fmax barre longitudinali
	passo delle staffe	p £ 15 Fmin barre longitudinali
		p £ 25 cm

NOTA: per i pilastri prefabbricati in stabilimento, i diametri minimi delle barre longitudinali e delle staffe sono rispettivamente ridotti a 10 mm e 5 mm.

3) setti e pareti:

Per strutture in c.a. intese come setti e pareti. di importanza corrente, sottoposte prevalentemente a sforzo assiale, quando la compressione media risulti non superiore al seguente limite

essendo "s" lo spessore della parete e "s^*_b" la tensione ammissibile, si potranno adottare per le armature da disporre su entrambe le facce le seguenti limitazioni dimensionali:

barre longitudinali	diametro minimo:	Fmin = 8 mm
	interasse massimo:	imax £ 30 cm
barre trasversali	diametro minimo:	Fmin = 5 mm
	interasse massimo:	imax £ 30 cm
		imax £ 20 Fbarre longitudinali

elementi di collegamento tra le due armature disposte su facce parallele: n. 6 per mq di parete

4) pilastri cerchiati

Nelle strutture semplicemente compresse, armate con ferri longitudinali disposti lungo una circonferenza e racchiusi da una spirale di passo non maggiore di 1/5 del diametro del nucleo cerchiato, si può assumere come area ideale resistente quella del nucleo, aumentata di 15 volte quella della sezione delle barre longitudinali e di 30 volte quella della sezione di un'armatura fittizia longitudinale di peso uguale a quello della spirale. L'area ideale così valutata non deve superare il doppio dell'area del nucleo. La sezione dell'armatura longitudinale non deve risultare inferiore alla metà di quella dell'armatura fittizia corrispondente alla spirale.

A'a	area fittizia di un'armatura longitudinale equipesante della spirale
Ac	area del nucleo cerchiato
Aci	area ideale del calcestruzzo
D	diametro esterno

Limiti da osservare in fase di progettazione e verifica:

5) instabilità flessionale dei pilastri (pilastri caricati di punta)

I fenomeni di instabilità flessionale devono essere presi in considerazione per snellezze

essendo "L_o" la lunghezza libera di inflessione ed "i" il corrispondente raggio di inerzia.

5.1) lunghezza libera di inflessione in funzione dei vincoli alle estremità delle aste:

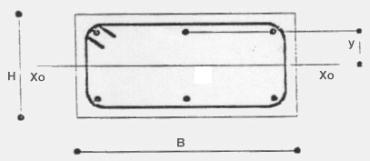
5.2) raggio minimo d'inerzia della sezione

il raggio minimo di inerzia della sezione è uguale a:

essendo:

(momento di inerzia della sezione omogeneizzata rispetto all'asse Xo-Xo

A_ci (area ideale del calcestruzzo come sopra definita)

Nel caso in cui il pilastro si carica di punta, il progetto e la verifica si effettuano amplificando il carico "N" per un coefficiente "w" tabellato in funzione della snellezza "l", per valori compresi tra 50 e 100.

I valori intermedi di "w" si ottengono per interpolazione lineare.

Snellezze maggiori di 100 sono da considerare con particolari cautele di progettazione e di calcolo.

La verifica viene eseguita nel piano di massima snellezza.

Snellezza	Coefficiente di amplificazione "w"
50 70 85 100	1.00 1.08 1.32 1.62

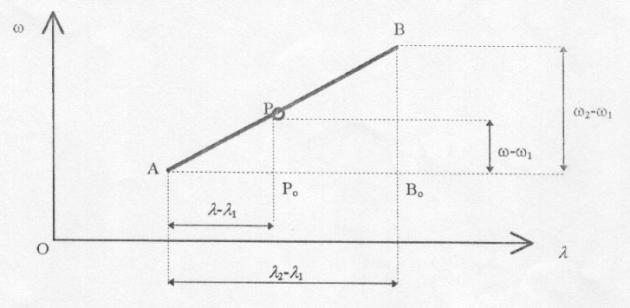
L'interpolazione lineare consiste nel determinare le coordinate di un punto P(l; w) giacente su una retta passante per due punti di note coordinate A(l₁; w₁) e B(l₂; w₂):

L'equazione della retta passante per i punti assegnati A e B, come è noto dalla geometria analitica, si determina dalla similitudine dei triangoli APPo e ABBo:

da cui si ricava: